算法第三讲排序(sort)

排序算法：将集合中的元素按照某种大小方式排列。

对于排列算法涉及到的操作和性能分析：

1. 元素之间大小关系的比较。- 比较的次数
2. 对于没有正确排列的元素，交换元素。 - 交换的次数[1]

目录

冒泡排序

bubble-sort思路：每一次交换都将元素向它的正确位置移动。

1. 在list中依次比较相邻两元素，如果不符合顺序就交换元素位置。重复多次，list中最大元素会被交换到list尾。
2. 一轮一轮的对list剩下的n-1、n-2、…、2个未排序元素，重复1步操作。

def bubble_sort(alist):
    for n in range(len(alist), 0, -1):
        for i in range(n-1):
            if alist[i] > alist[i+1]:
                alist[i], alist[i+1] = alist[i+1], alist[i]
>>> alist = [54,26,93,17,77,31,44,55,20]
>>> bubble_sort(alist)
>>> print(alist)
>>> [17, 20, 26, 31, 44, 54, 55, 77, 93]

冒泡算法需要一轮一轮的比较和交换。如果在某一轮比较中没有一次交换，说明剩下的元素也已经都排序过了。多了这个检查步骤的冒泡排序：short-bubble-sort。

def short_bubble_sort(alist):
    exchange = True
    n = len(alist) - 1
    while n > 0 and exchange:
        exchange = False
        for i in range(n):
            if alist[i] > alist[i+1]:
                exchange = True
                alist[i], alist[i+1] = alist[i+1], alist[i]
        n = n - 1

复杂度：O(n**2)。需要比较的次数：(n-1) + (n-2) + … + 1。

选择排序

selection-sort思路：大致思路和bubble-sort一样，只是不用每次相邻元素比较后就交换位置。

1. 每一轮，在list中，找到未排序元素中最大元素所在位置，直接交换到未排序list尾部。
2. 一轮一轮的对list剩下的n-1、n-2、…、2个未排序元素，重复1步骤。

def selection_sort(alist):
    for n in range(len(alist)-1, 0, -1):
        position_of_max = 0
        for i in range(1, n+1):   # 找到未排序元素中最大元素所在位置
            if alist[i] > alist[position_of_max]:
                position_of_max = i
        # 交换到未排序list的尾部
        alist[n], alist[position_of_max] = alist[position_of_max], alist[n]

复杂度：O(n**2)。和bubble-sort相比，元素间比较的次数不变，只是交换的次数减少。

插入排序

insertion-sort思路：维持一个排序好的子序列，每一轮将下一个数插入到这个子序列中正确的位置。

1. 每一轮，在list中，找到第n个元素在排序好的前n-1个元素序列中的位置。(通过依次和前一个元素比较，小于前一个元素，前一个元素就往后移动一格；大于，就找到位置)
2. n从2到N

def insertion_sort(alist):
    for n in range(1, len(alist)):  # 未排序的元素
        current_value = alist[n]    # 待被插入的元素
        position = n
        while position > 0 and alist[position-1] > current_value:  # 找到第一个比它小的元素，找到了插入的位置
            alist[position] = alist[position-1]    # 这里一定要一步步的移动，留一个空位子
            position = position - 1
        alist[position] = current_value

复杂度：O(n**2)

希尔排序

shell-sort思路：将list分解为多个小的子list，每个子list使用插入排序。希尔排序使用增量gap来选择子list。

1. 对list而言，从gap为n/2开始，依次n/4,…,1。

def shell_sort(alist):
    # do the insert sort
    def gap_insertion_sort(alist, start, gap):
        for i in range(start+gap, len(alist), gap):
            value = alist[i]
            pos = i
            while pos >= gap and alist[pos-gap] > value:
                alist[pos] = alist[pos-gap]
                pos = pos - gap
            alist[pos] = value
    gap = len(alist) // 2
    while gap > 0:
        for start in range(gap):
            gap_insertion_sort(alist, start, gap)
        gap = gap // 2

复杂度：O(n**2)

归并排序

merge-sort思路：分而治之的策略，递归的方式实现。

1. 将list拆成两半递归调用归并排序。base情况为：拆分后的子列表只有一项（递归中的base概念）
2. 将1中归并排序过的两个子list合并成一个排序过的新list。找到left和right中最小的元素依次向新list里面放。（这时候会用到额外的存储空间）[2]

def merge_sort(L):
    def merge(left, right):
        result = []
        while left or right:
            if (not left) or (right and left[0] > right[0]):
                result.append(right.pop(0))
            else:
                result.append(left.pop(0))
        return result
    if len(L) <= 1:  # base
        return L[:]
    mid = len(L) / 2
    left, right = merge_sort(L[:mid]), merge_sort(L[mid:])
    return merge(left, right)
>>> alist = [54,26,93,17,77,31,44,55,20]
>>> print(merge_sort(alist))
>>> [17, 20, 26, 31, 44, 54, 55, 77, 93]

复杂度：O(NlogN)。

• 拆分过程：list被分成两半，将长度为N的list一直分到长度为1的，需要经过logN次。
• 合并过程：left+right长度为N的一次merge需要经过N个操作合并成一个result。

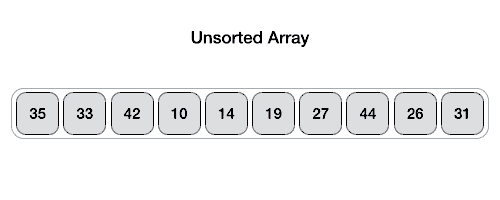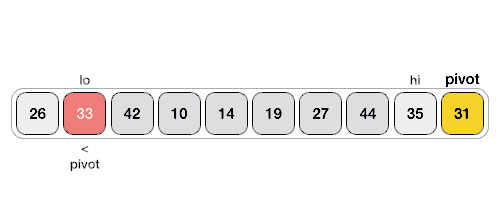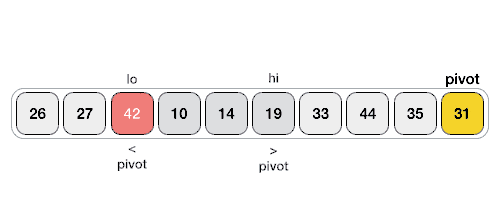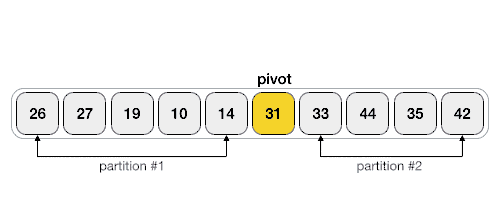
快排序

quick-sort思路：同归并排序一样，使用分而治之的策略。与归并不同，归并选择一个位置来把list分半，快排选择一个值（中轴值）来把list分半。

1. 选择list中list[0]为中轴值。找到中轴值的位置，保证左半部分小于中轴值，右半部分大于中轴值。然后左半部分，有半部分递归调用。
2. partition部分：找位置，小值在左边，大值在右边（实现方法很多)：
   • 方法一：left向右移动找到第一个大于list[0]，right向左移动找到第一个小于list[0]的值交互。直到left和right交叉。（gif图是这种）
   • 方法二：pivot是中轴值value最终的位置，遍历list[1]到list[-1]，找到一个小于value的pivot位置就应该向后移动一位。

def quick_sort(L, first=0, last=None):
    def partition(L, begin, end):
        pivot = begin        # 中轴值位置初始化
        value = L[begin]     # 中轴值
        for i in range(begin+1, end+1):
            if L[i] < value:
                pivot += 1
                L[i], L[pivot] = L[pivot], L[i] # 把小于的值移动到pivot位置前面
        # 此时pivot位置上的值一定小于或等于中轴值value，这里把begin位置上的中轴值移动到pivot位置上
        L[pivot], L[begin] = L[begin], L[pivot]
        return pivot

    last = len(L)-1 if last == None else last
    if first >= last: # base
        return
    pivot = partition(L, first, last) # split point
    quick_sort(L, first, pivot-1)
    quick_sort(L, pivot+1, last)

复杂度：O(NlogN)

堆排序

** 待序 **

动画

冒泡排序：

选择排序：

插入排序：

希尔排序：

youtube

归并排序：

快排序：

堆排序：

参考资料：

• Problem Solving with Algorithms and Data Structures - Chapter 5

扩展阅读：

• Color Visualization of Sorting Algorithms

注[1]: 交换不同位置的两个元素，可能涉及到很多次两两元素交换。

注[2]：第一次实现merge-sort时的merge方法。

...
    def merge(left, right):
        result = []
        i, j = 0, 0
        while i < len(left) and j < len(right):
            if left[i] < right[j]:
                result.append(left[i])
                i += 1
            else:
                result.append(right[j])
                j += 1
        if i < len(left):
            result.extend(left[i:])
        elif j < len(right):
            result.extend(right[j:])
        return result
    ...

注[3]: Animated Algorithms、数据结构和算法可视化、算法动画图解 - APP